Esercitazione 3

Reti sincronizzate

Le reti sincronizzate sono reti logiche con uno stato interno, mantenuto usando registri, che si evolvono a instanti discreti dati da un segnale di clock. In questa esercitazione vedremo come realizzarle, simularle e studiarle nell'ambiente d'esame.

Testbench e generatore di clock

Per poter simulare una rete sincronizzata dobbiamo innanzitutto avere un generatore di clock. Il segnale di clock è segnale oscillante, che dal punto di vista logico appare come in figura.

Clock in realtà

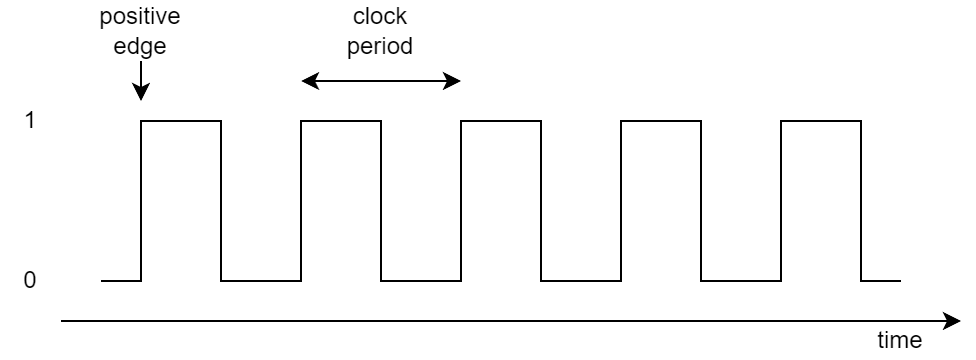
In realtà i generatori di clock sono basati su cristalli di quarzo, un materiale piezoelettrico con il quale si possono realizzare circuiti oscillanti. Questi circuiti emettono una tensione oscillante come mostrato in figura (da Wikimedia), notare come l'onda sia molto meno squadrata di quanto presentato al livello logico.

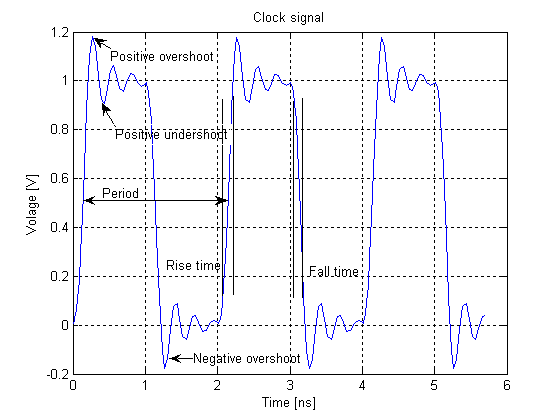
Per i nostri usi, ci basterà descrivere una rete asincrona che cambia il proprio segnale da 0 a 1, e viceversa, ad intervalli regolari. Una qualunque descrizione realistica, e dunque sintetizzabile, dovrebbe avere a che fare con un segnale di reset che indichi a questa rete da che punto cominciare. Dato che però vogliamo usare questo generatore in una testbench simulativa, possiamo utilizzare direttamente i concetti relativi, approfittando della keyword initial per mantenere il codice semplice.

// generatore del segnale di clock
module clock_generator(
    clock
);
    output clock;

    parameter HALF_PERIOD = 5;

    reg CLOCK;
    assign clock = CLOCK;

    initial CLOCK <= 0;
    always #HALF_PERIOD CLOCK <= ~CLOCK;

endmodule

Notiamo che questa rete non è sintetizzabile. Infatti, utilizza la keyword initial, che è priva di senso in hardware, e un reg non come registro ma come variabile, come già visto nelle testbench. Questo si nota dal fatto che il reg non viene aggiornato in risposta ad un altro segnale, come il positive edge del clock, come invece accade per registri.

Periodo del clock

Il parametro HALF_PERIOD rende il periodo di questo generatore di clock configurabile. Tipicamente all'esame viene utilizzato il valore default di 5, che implica periodi di clock di 10 unità di tempo. Qualora questo cambiasse (per esempio, per permettere reti combinatorie con maggior tempo di attraversamento) sarà segnalato nel testo.

Come ogni altra rete, questa viene inclusa nella testbench con una instanziazione.

module testbench();
    wire clock;
    clock_generator clk(
        .clock(clock)
    );
    ...
    mia_rete dut(
        ...
        .clock(clock)
    );
    ...

Oltre al segnale di clock, una rete sincronizzata avrà bisogno anche del segnale di reset. Questo viene aggiunto come un reg pilotato all'inizio del blocco initial della testbench.

module testbench();
    ...
    reg reset_;
    ...
    mia_rete dut(
        ...
        .clock(clock), .reset_(reset_)
    );
    ...
    initial begin
        reset_ = 0;
        #(clk.HALF_PERIOD);
        reset_ = 1;
        ...
    end

Con la sintassi #(clk.HALF_PERIOD); si attendono unità di tempo proporzionali al periodo di clock configurato. Questo è utile ad evitare di modificare manualmente tutte le attese in caso di cambio di clock.

Primo esempio di rete sincronizzata: il contatore

Vediamo ora un semplice esempio di rete sincronizzata, un contatore. Questa rete ha un registro di 3 bit inizializzato a 0, che viene incrementato ad ogni ciclo di clock, facendo infine wrap-around da 7 a 0. Il codice è scaricabile qui.

module contatore (
    out,
    clock, reset_
);
    output [2:0] out;
    input clock, reset_;

    reg [2:0] OUT;
    assign out = OUT;

    always @(reset_ == 0) begin
        OUT <= 0;
    end

    always @(posedge clock) if (reset_ == 1) #3 begin
        OUT <= OUT + 1;
    end
endmodule

Vediamo quindi come questo codice modella il comportamento di una vera rete sincronizzata. Il reg OUT viene collegato direttamente all'uscita out, viene inizializzato a 0 solo in corrispondenza del segnale di reset (righe 11-13) e, durante la normale operazione, viene aggiornato con il valore OUT + 1 in corrispondenza di un posedge del clock. Il ritardo #3 modella il tempo $T_{propagation}$ del registro.

Assegnamento con <=

È importante, nelle reti sincronizzate, utilizzare <= per assegnamenti a registri sul fronte positivo del clock. Questo perché gli statement con <= sono intesi come eseguiti in parallelo, non sequenzialmente. Infatti, i registri non sono variabili e i loro cambiamenti non sono visibili agli altri registri fino al successivo posedge del clock.

Possiamo vedere come si evolve questa rete, simulandola in una testbench con segnale di clock e reset_ (scaricabile qui). Per il resto, la testbench non fa altro che attendere diversi cicli di clock, visto che questa rete non ha alcun input e si evolve in autonomia.

Vediamo l'evoluzione della rete usando GTKWave.

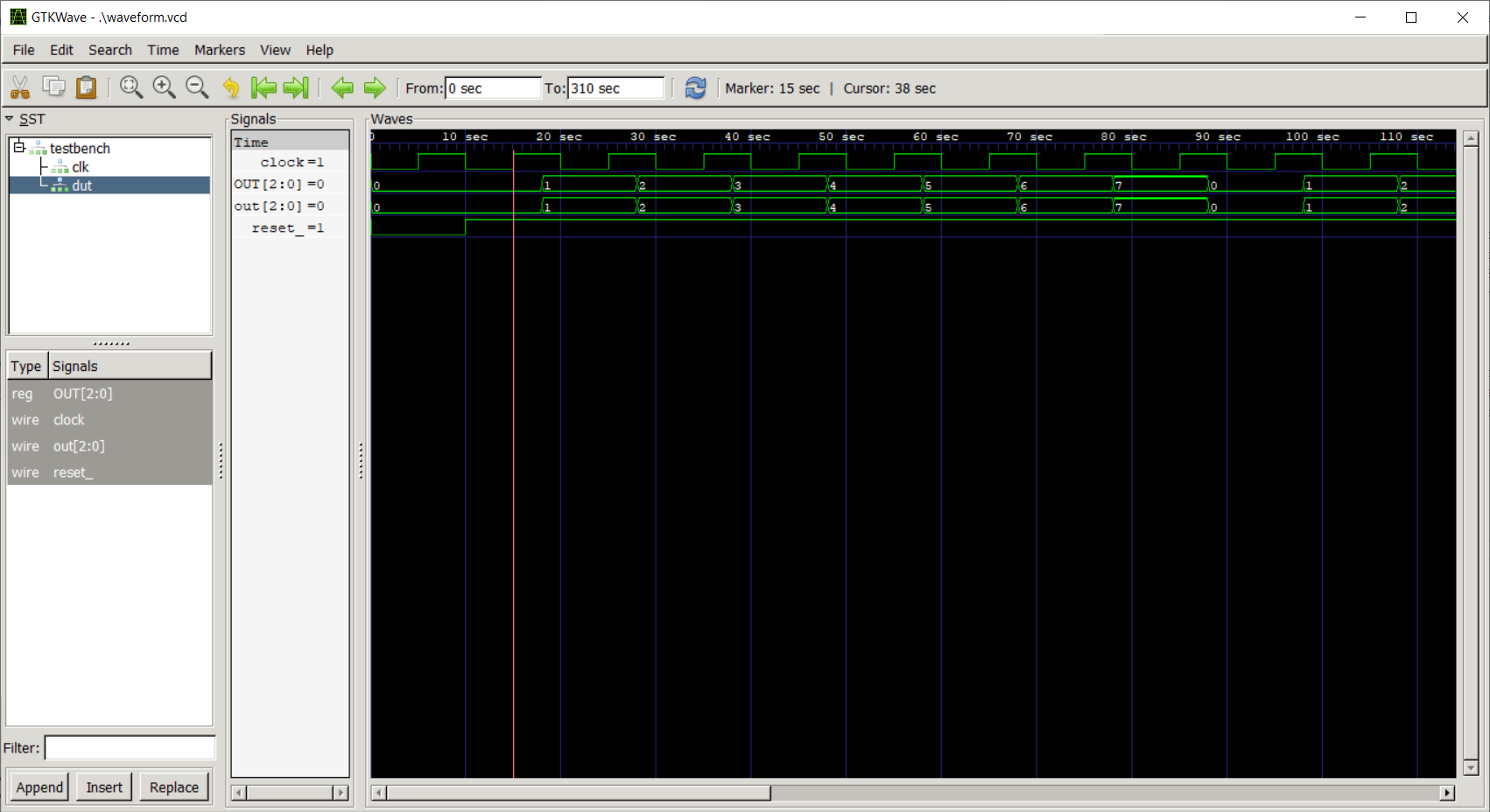
Osserviamo, in particolare, il registro OUT e il segnale del clock. Notiamo che a ogni fronte positivo del clock, OUT non cambia immediatamente, ma solo dopo 3 unità di tempo.

Dalla teoria sui registri, ricordiamo anche che il nuovo valore assunto dal registro deve essergli dato in input da $T_{setup}$ prima del posedge e fino a $T_{hold}$ dopo il posedge. Questo però non si nota da questa waveform: non c'è nulla che rappresenta il valore in ingresso al registro prima del posedge. Torniamo al codice: alla riga 16 usiamo una espressione combinatoria a sinistra dell'assegnamento. Questa espressione viene calcolata dal simulatore Verilog al momento dell'assegnamento, cioè $t_{posedge} + 3$, e non prima. Ciò significa che il simulatore non sta simulando né il risultato combinatorio in ingresso al registro, né il fatto che sia settato e mantenuto per i giusti tempi.

Possiamo ovviare al primo di questi problemi introducendo un wire, che ci rappresenti la rete combinatoria che calcola il successivo valore di OUT (scaricabile qui).

module contatore (
    out,
    clock, reset_
);
    output [2:0] out;
    input clock, reset_;

    reg [2:0] OUT;
    assign out = OUT;

    wire [2:0] next_out;
    assign #2 next_out = OUT + 1;

    always @(reset_ == 0) begin
        OUT <= 0;
    end

    always @(posedge clock) if (reset_ == 1) #3 begin
        OUT <= next_out;
    end
endmodule

Simulando questa nuova rete, otteniamo la seguente waveform.

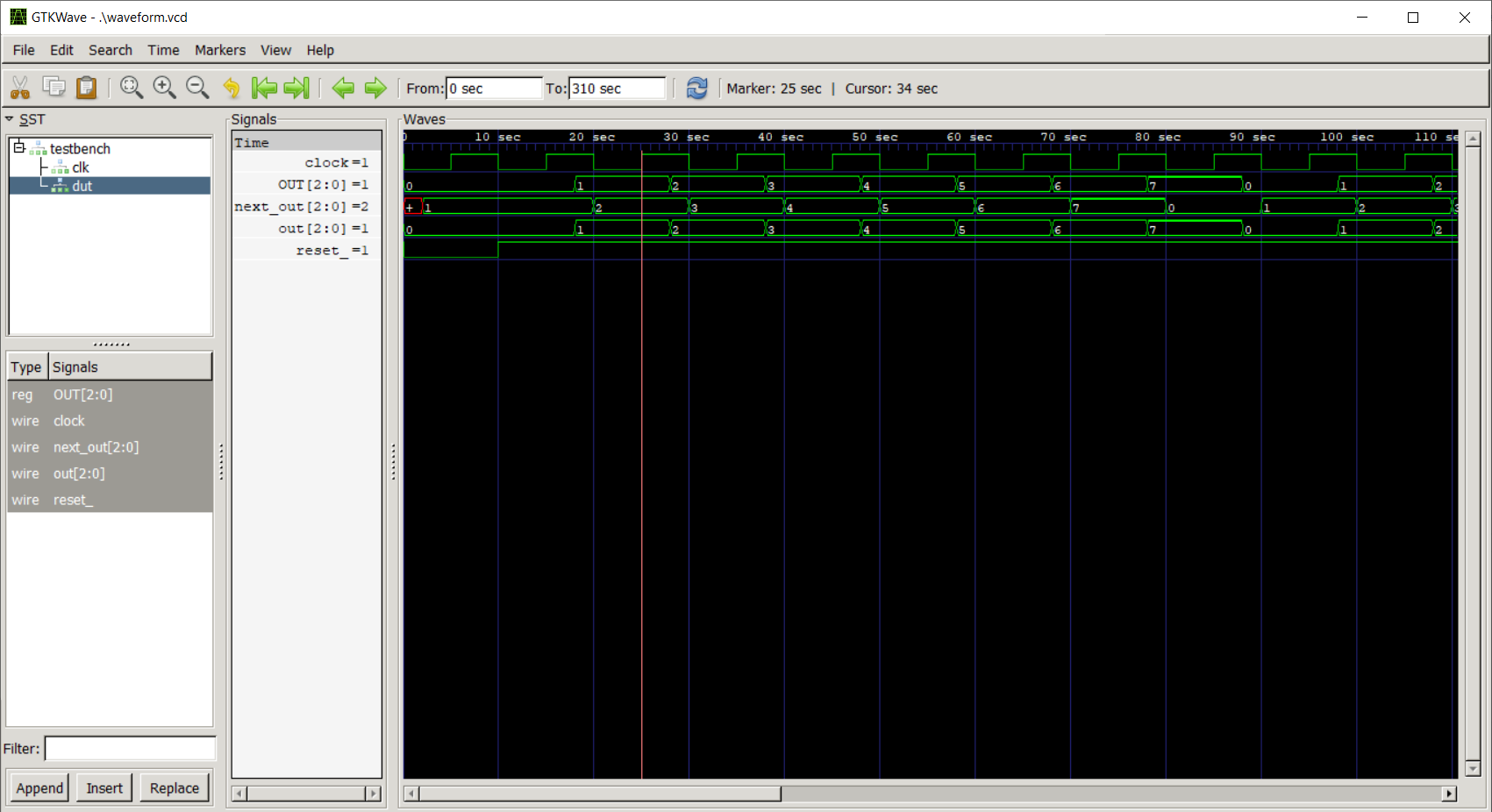
Vediamo ora chiaramente che la rete combinatoria che produce next_out risponde quasi immediatamente, ma il registro OUT non registrerà il suo valore fino al prossimo posdege del clock. Infatti, il periodo che separa due posedge è utilizzato proprio per far propagare i nuovi valori dei registri attraverso reti combinatorie, che andranno a produrre i nuovi ingressi dei registri che questi registreranno al prossimo posedge.

Questo modo di propagarsi dei valori tra un ciclo di clock è l'altro è fondamentale per capire come funzionano le reti sincronizzate ed essere quindi in grado di scrivere Verilog corrispondente alla macchina a stati che vogliamo realizzare. Allo stesso modo, riuscire a leggere questa evoluzione dalla waveform è fondamentale per rendere queste utili al debugging.

Mantenere un segnale per N cicli di clock

Vediamo ora l'esempio di una rete sincronizzata con uscita out a 1 bit, che, ciclicamente, viene tenuta a 1 per N clock e messa a 0 per 1 clock. Il codice è scaricabile in due versioni, qui senza wire di debug e qui con, mentre la testbench è qui.

Per semplicità, discutiamo direttamente la versione che usa wire di debug per evidenziare gli ingressi dei registri.

module out_n_clock(
    out,
    clock, reset_
);
    output out;
    input clock, reset_;

    reg OUT;
    assign out = OUT;

    localparam N = 3;
    reg [3:0] COUNT;

    reg STAR;
    localparam S0 = 0, S1 = 1;

    always @(reset_ == 0) begin
        COUNT <= N;
        OUT <= 0;
        STAR <= S0;
    end

    wire [3:0] next_count_s0;
    assign #2 next_count_s0 = COUNT - 1;

    wire next_star_s0;
    assign #2 next_star_s0 = (COUNT == 1) ? S1 : S0;
    
    always @(posedge clock) if (reset_ == 1) #3 begin
        casex (STAR)
            S0: begin
                COUNT <= next_count_s0;
                OUT <= 1;
                STAR <= next_star_s0;
            end

            S1: begin
                COUNT <= N;
                OUT <= 0;
                STAR <= S0;
            end
        endcase
    end
endmodule

Questa rete inizializza COUNT a N e, in S0, lo decrementa continuamente. Anziché saltare da S0 a S1 quando COUNT raggiunge 0, lo facciamo invece quando raggiunge 1. Perché? Guardiamo la waveform per capirlo meglio.

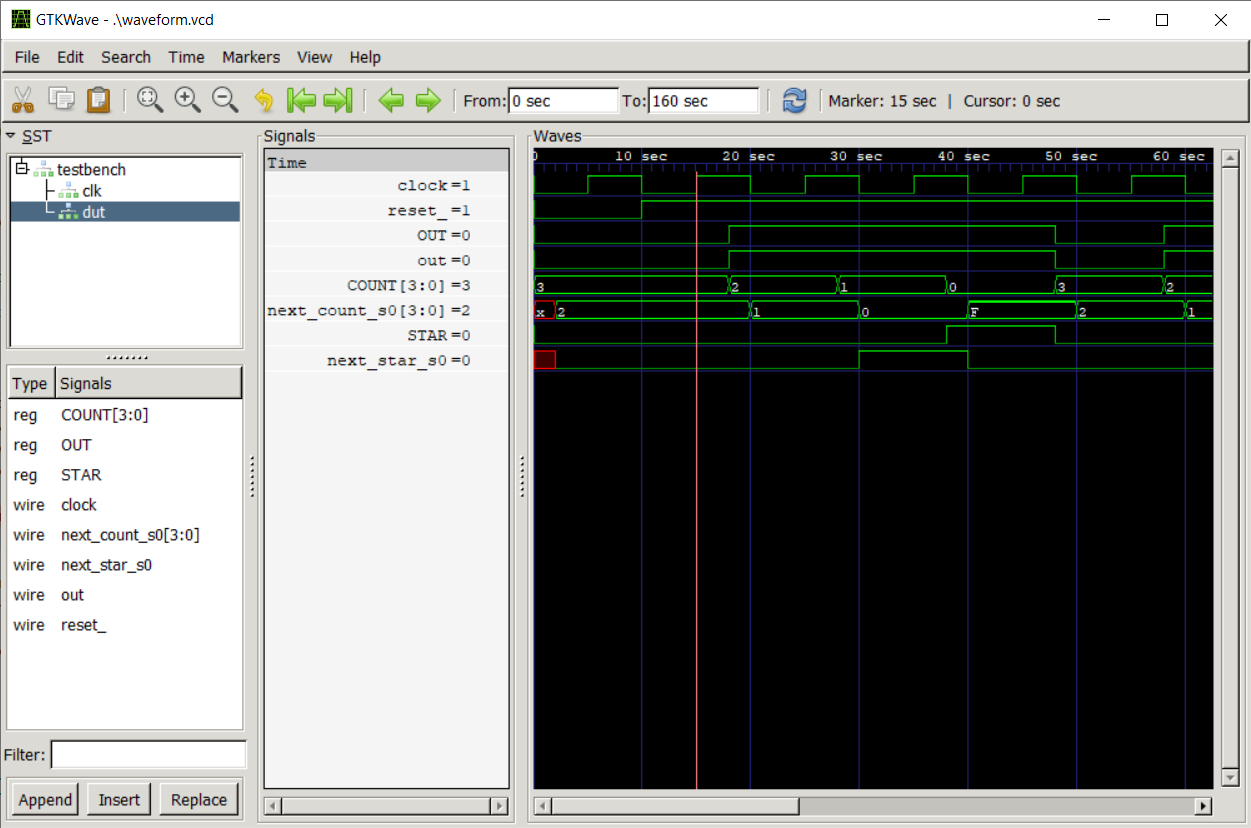
A $t = 15$ corrisponde il primo posedge del clock con reset_ a 1. Notiamo che a questo punto OUT è a 0 per via dell'inizializzazione, ma a $t = 18$ questo passa a 1, conseguenza della riga 33. Per COUNT, invece, notiamo che è stato inizializzato a 3, e subito dopo next_count_s0 ha calcolato 2 come prossimo valore. A $t = 18$, COUNT decrementa a 2.

Passiamo ora al clock successivo, cioè $t = 25$. COUNT vale 2, assume poco dopo valore 1, a $t = 28$. Notiamo next_star_s0 a cavallo di questo cambiamento: subito dopo il passaggio di COUNT a 1, next_star_s0 diventa S1. Siamo però a $t = 30$, non $t = 25$: il check sul valore di COUNT non cambia fino a dopo il posedge del clock, e quindi STAR rimane S0 per un altro ciclo. Al ciclo dopo, a $t = 38$, vediamo che lo stato passa dunque a S1, ma OUT resta 1: infatti solo al clock dopo il cambio di stato avrà effetto sui registri, compreso COUNT che reinizializzato. Guardando il filo OUT in tutto ciò, notiamo che è rimasto effettivamente a 1 per N = 3 cicli di clock, come da specifica.

Ci sono diversi fattori che possiamo cambiare, ottentendo risultati diversi. Se inizializziamo COUNT a N - 1, seguendo la stessa logica dovremmo contare fino a 0. Se anticipiamo il cambio di OUT, usando OUT <= (COUNT == 1) ? 0 : 1, allora si perde il ciclo in più con OUT a 1 e dovremmo cambiare il conteggio di conseguenza. Anche per strutture apparentemente così semplici, è quindi possibile combinare tanti approcci diversi al punto tale che è difficile dedurre a colpo d'occhio la durata del segnale. È per questo importante sapere come si evolvono i vari registri, come si propagano i loro cambi di valori, come ricostruire (e leggere) una waveform.

Partire da N bassi

Nello ragionare su comportamenti di questo tipo, che sia a mente o su carta, è una buona idea partire da N bassi, come 1 o 2, e calcolare la durata del segnale in termini di N. Per esempio, in questo esercizio abbiamo visto che inizializzando COUNT a N otteniamo OUT a 1 per N cicli di clock. Questo varrà che N sia 3 o che sia 12, ma N = 3 è molto più rapido da verificare, e N = 2 lo è ancora di più.

Esercizio: Handshake e reti combinatorie

Vediamo un esempio di semplice esercizio che segue uno schema tipico all'esame. Il testo è scaricabile qui.

La testbench è più complessa di quanto visto finora, nella prossima sezione vedremo le principali caratteristiche utili per debugging. Per ora, vediamo come si realizza una rete che risponde a queste specifiche.

Il testo ci chiede di eseguire un handshake dav/rfd con il produttore. Questo handshake prevede che, tramite il filo rfd ("ready for data") che va dal consumatore al produttore e il filo dav_ ("data valid", attivo basso) che va dal produttore al consumatore, questi si coordinino per la corretta trasmissione del dato. Ricordiamo i passi di questo protocollo:

• A riposo: dav_ = 1, rfd = 1.
• Comincia il produttore: dav_ = 0. Questo segnala che il dato è valido.
• ACK del consumatore: rfd = 0. Questo segnala che il dato è stato letto.
• Reset del produttore: dav_ = 1.
• Reset del consumatore: rfd = 1.

Un protocollo, in generale, descrive come due o più attori devono interagire tra loro. Quando implementiamo un attore di un protocollo, ci sono due punti importanti da ricordare perché questo funzioni:

1. vanno eseguiti tutti gli step che ci competono, quando il protocollo ci dice di farlo;
2. quando il protocollo dice che qualcun'altro deve segnalare qualcosa, dobbiamo attendere che questo accada.

In questo esercizio, implementiamo il consumatore, che deve prelevare un dato dal produttore. Rileggiamo quindi il protocollo di sopra dal punto di vista del consumatore, per capire cos'è che dobbiamo fare nella nostra rete.

• A riposo, e in particolare al reset iniziale: rfd = 1.
• Attendiamo che il produttore segnali dav_ = 0.
• Leggiamo il dato.
• Comunichiamo l'avvenuta lettura con rfd = 0.
• Attendiamo che il produttore segnali dav_ = 1.
• Segnaliamo il reset del protocollo con rfd = 1.

Dall'altra parte, una volta ottenuto il dato valido per a e b, svolgiamo il conto prescritto utilizzando una rete combinatoria e ne emettiamo il risultato tramite l'uscita p.

Ordine delle operazioni

Non c'è nessuna prescrizione rigida sull'ordine delle operazioni tra gli step del protocollo e l'immissione del dato in uscita. È valido sia completare l'handshake fino al suo reset e poi trasmettere il dato, sia trasmettere immediatamente il dato e poi chiudere l'handshake.

La testbench dovrà tenere conto di ciò.

Nello svolgere il calcolo, dobbiamo implementare una semplice rete combinatoria. L'aspetto più interessante è come usarla: dobbiamo assicurarci di campionarne l'output solo quando gli input relativi sono validi.

Da questi ragionamenti, deriviamo la seguente descrizione, scaricabile qui.

module ABC(
    a, b, p,
    dav_, rfd,
    clock, reset_
);
    input [3:0] a, b;
    output [5:0] p;

    input dav_;
    output rfd;

    input clock, reset_;

    reg [5:0] P;
    assign p = P;

    reg RFD;
    assign rfd = RFD;

    reg [3:0] A, B;

    wire [5:0] out_rc;
    PERIMETRO_RC rc(
        .a(A), .b(B),
        .p(out_rc)
    );

    reg [2:0] STAR;
    localparam 
        S0 = 0, 
        S1 = 1,
        S2 = 2, 
        S3 = 3;
    
    always @(reset_ == 0) begin
        RFD <= 1;
        P <= 0;
        STAR <= S0;
    end

    always @(posedge clock) if (reset_ == 1) #3 begin
        casex (STAR)
            S0: begin
                A <= a;
                B <= b;
                STAR <= (dav_ == 0) ? S1 : S0;
            end 

            S1: begin
                P <= out_rc;
                STAR <= S2;           
            end  

            S2: begin
                RFD <= 0;
                STAR <= (dav_ == 1) ? S3 : S2;
            end

            S3: begin
                RFD <= 1;
                STAR <= S0;
            end
        endcase
    end
endmodule

module PERIMETRO_RC(
    a, b,
    p
);
    input [3:0] a, b;
    output [5:0] p;

    wire [4:0] somma;
    add #( .N(4) ) adder(
        .x(a), .y(b), .c_in(1'b0),
        .s(somma[3:0]), .c_out(somma[4])
    );
    assign p = { somma[3:0], 1'b0 };
endmodule

Testbench con input e output per reti sincronizzate

Ci muoviamo ora verso reti sincronizzate più complesse, che prendono input da altre reti, svolgono conti, ed emettono output.

Blocchi in parallelo: fork ... join

Per scrivere testbench per reti combinatorie abbiamo sfruttato la loro inerente semplicità: dato un nuovo ingresso, una rete combinatoria emette l'output corrispondente dopo un certo tempo. Questo output non varierà nel tempo finché manteniamo l'input costante, anzi in ogni caso allo stesso input corrisponde lo stesso output. Questo ci permette di scrivere testbench semplici basate sulla struttura 1) assegno gli ingressi, 2) attendo un tempo sufficiente, 3) controllo le uscite.

Questo non è però fattibile con le reti sincronizzate: ad un singolo ingresso possono corrispondere diversi cambi di stato ed uscite diverse, e il tempo necessario al calcolo è difficilmente prevedibile. Inoltre, se la rete si coordina tramite handshake con altre reti, non si può determinare a priori in quale ordine eseguirà questi hadnshake. È necessario quindi adottare una struttura che permette a ciascun componente con cui la rete testata interagisce di comportarsi come un componente indipendente che non è bloccato dal proseguire degli altri - proprio come hardware vero.

Questo è possibile con il costrutto fork ... join. All'interno di un fork ... join possiamo definire diversi blocchi begin ... end il cui codice verrà eseguito indipendentemente e in parallelo. Possiamo quindi sfruttare questo per rappresentare diversi componenti.

fork
    begin : Producer_1
        ...
    end

    begin : Producer_2
        ...
    end

    begin : Consumer
        ...
    end
join

All'interno dei blocchi Producer scriveremo codice per fornire dati di input alla rete, all'interno dei blocchi Consumer scriveremo codice per ottenere i dati di output della rete e verificare che questi corrispondano a quanto atteso.

Timeout di simulazione

Un tipo di problema che possiamo incontrare nelle reti sincronizzate ma non nelle reti combinatorie è la situazione in cui un componente resta in attesa di un segnale che in realtà non verrà mai emesso. Per esempio, questo avviene se la rete da noi realizzata non rispetta il protocollo di handshake.

In questi casi, la simulazione può proseguire indefinitivamente.

È quindi necessario prevedere un meccanismo di timeout che interrompe la simulazione quando questa stia durando molto più di quanto è ragionevole aspettarsi. Possiamo realizzare questo utilizzando sempre fork ... join.

//the following structure is used to wait for expected signals, and fail if too much time passes
fork : f
    begin
        #100000;
        $display("Timeout - waiting for signal failed");
        disable f;
    end
    //actual tests start here
    begin 
        //reset phase
        ...

        fork
            begin : Producer_1
                ...
            end

            begin : Producer_2
                ...
            end

            begin : Consumer
                ...
            end
        join
    end
join

$finish;

Combinando disable f, che interrompe ogni esecuzione all'interno del fork ... join iniziale, e $finish dopo di questo ci assicuriamo che quando il timeout è raggiunto la simulazione viene terminata. Questo ci lascerà una waveform che potremo analizzare per capire da dove sia scaturito il blocco.

Linee di errore

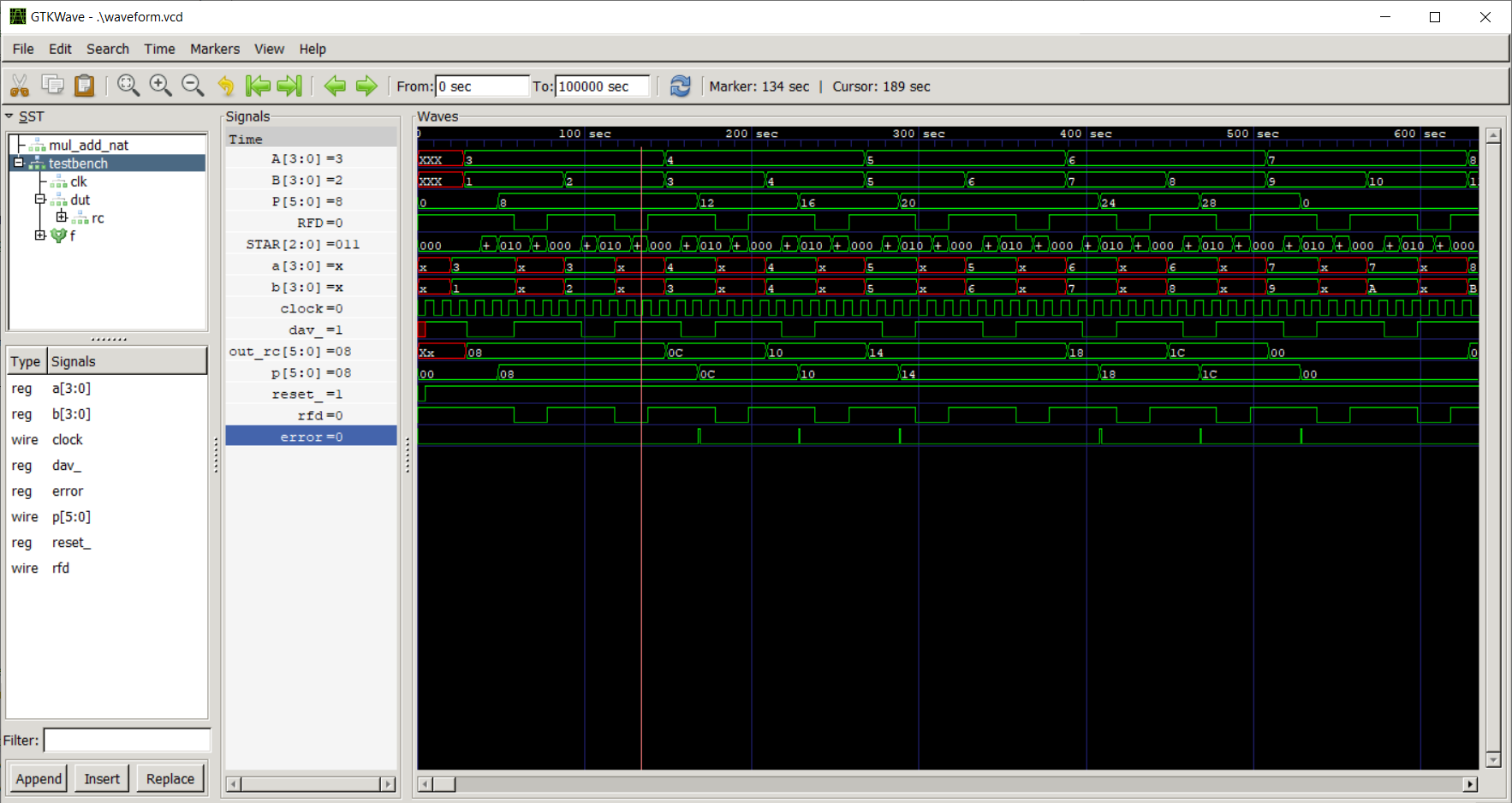
Le simulazioni di reti sincronizzate possono essere molto lunghe (in termini di tempo simulativo, non tempo reale) producendo di conseguenza waveform molto lunghe. Analizzare queste waveform in cerca di errori può essere molto tedioso. Per questo, le testbench d'esame includono solitamente delle linee di errore, che evidenziano a colpo d'occhio dov'è che sia avvenuto un problema.

Queste linee sono realizzate nella testbench con una variabile reg error inizializzata a 0 ed un blocco always che risponde ad ogni variazione di error per rimetterla a 0 dopo una breve attesa. Questa attesa breve ma non nulla fa sì che basti assegnare 1 ad error per ottenere un'impulso sulla linea, facilmente visibile.

module testbench();
    ...
    initial begin
        ...
    end

    reg error;
        initial error = 0;
    always @(posedge error) #1
        error = 0;
endmodule

Possiamo quindi scrivere un check dell'output come segue.

if(p != t_p) begin
    $display("Expected %d, received %d", t_p, p);
    error = 1;
end

In GTKWave, guarando alla linea error della testbench questi punti saranno facilmente identificabili nella waveform, come dall'esempio seguente.